Luminescent diradicals

Felix

π-conjugated diradicals can possess unique luminescence properties if their zwitterionic states are harnessed. Crucially, if S0 and T1 form a quasidegenerate ground state, then the first excited state of such a system is a singlet. This, in turn, can be used to reduce triplet loss channels. The full story here:

Near-infrared luminescent open-shell π-conjugated systems with a bright lowest-energy zwitterionic singlet excited state, which just appeared in Science Advances.

Planar chromophore design

Felix

It is by now fairly well understood how chromophore properties are affected by push/pull substituents and their degree of planarity. But how can we rationalise variations in the properties of planar chromophores that do not possess charge transfer character?

We were interested in understanding the apparent differences between these two isomeric molecules (called the Pechmann dyes).

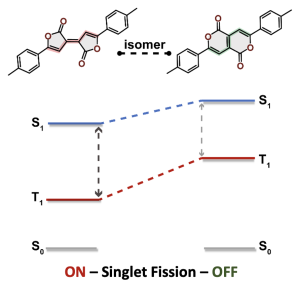
Why is the T1 of PM5 (shown to the left) so much lower than the one of PM6 (shown to the right) making PM5 a powerful candidate for a singlet fission material whereas the S1/T1 gap of PM6 is too small for this purpose?

The answer is discussed in the new paper “Singlet Fission in Pechmann Dyes: Planar Chromophore Design and Understanding” that just appeared in JACS.

The overall lower excitation energies of PM5 vs PM6 can be understood by the fact that the S1 and T1 of the former are stabilised via excited-state aromaticity whereas the S0 of the latter profits from ground-state aromaticity.

The reason for the lower S1/T1 gap in PM5 is more subtle but also more fascinating pointing to a whole new way of viewing excitation energies. We were able to highlight the effect of the double bond conformation in influencing the exchange integral between the excited electron and hole, which ultimately leads to the variations in S1/T1 gap.

Oscillator strengths

Felix

I find oscillator strengths intriguing. Let me just add a few thoughts to an earlier blogpost. We start with the two commutators

[x,\hat{p}_x]=\dfrac{\hbar}{i}

(1)

[x,\hat{H}]=-i\dfrac{\hbar}{m}\hat{p}_x

(2)

which can both be fairly easily derived. Taking Eq. (2), left multiplying by \left<\Psi_0 \right| and right multiplying by \left|\Psi_I \right> and assuming that they are both eigenfunctions, we get

E_I-E_0 = -i\dfrac{\hbar}{m}\dfrac{\left<\Psi_0\mid \hat{p}_x\mid\Psi_I\right>}{\left<\Psi_0\mid x\mid\Psi_I\right>}

(3)

For some, in my opinion very strange, reason it is the case that the energy gap between any two states is proportional to the ratio between their transition dipole moments in the velocity and length representations.

Starting with Eq. (1), left multiplying by \left<\Psi_0 \right| , right multiplying by \left|\Psi_0 \right> and inserting the resolution of the identity \sum_I\left|\Psi_I \right>\left<\Psi_I \right| we obtain

\dfrac{2}{i}\sum_I \text{Im}\left[ \left<\Psi_0 \right|\hat{p}_x\left|\Psi_I \right>\left<\Psi_I \right|x\left|\Psi_0 \right>\right] = \dfrac{\hbar}{i}

(4)

Now we define the oscillator strength in the mixed gauge as

f_{0I}^\text{mix} = \dfrac{2}{3\hbar}\sum_\alpha \text{Im}\left[ \left<\Psi_0 \right|\hat{p}_\alpha\left|\Psi_I \right>\left<\Psi_I \right|r_\alpha\left|\Psi_0 \right>\right]

(5)

where \alpha goes over the x, y, and z coordinates of all electrons (that is 3N terms in total). Reinserting into Eq. (4) yields the Thomas-Reiche-Kuhn sum rule

\sum_I f_{0I}=N

(6)

stating that the sum over all oscillator strengths starting from any given state is equal to the number of electrons. This means that the oscillator strength can be seen to represent the number of oscillating electrons in any given transition.

Using Eq. (3) we can also rewrite the oscillator strength in the more common length gauge

f_{0I}^\text{length} = \dfrac{2m}{3\hbar^2}(E_I-E_0)\sum_\alpha |\left<\Psi_0 \right|r_\alpha\left|\Psi_I \right>|^2

(7)

or the velocity gauge

f_{0I}^\text{veloc} = \dfrac{2}{3m}\dfrac{1}{(E_I-E_0)}\sum_\alpha |\left<\Psi_0 \right|\hat{p}_\alpha\left|\Psi_I \right>|^2

(8)

In the limit of a complete basis set, all three definitions of the oscillator strength lead to the same result. In this sense, one can use these definitions to see how much the basis set is converged.

The thing that I find strange is how the oscillator strength could either be independent of the energy gap [Eq. (5)], proportional to it [Eq. (7)], or inversely proportional [Eq. (8)]. If two states cross, should the oscillator strength go to zero according to Eq. (7) or diverge to infinity according to Eq. (8)?

Excited states of diradicals

Felix

Computations on diradicals are not only difficult in terms of choosing an appropriate electronic structure method but in many cases it is also quite challenging to make sense of the results obtained. To tackle this problem we developed a detailed characterisation scheme for the excited states of diradicals in our new paper Classification and quantitative characterisation of the excited states of π-conjugated diradicals that just appear in Faraday Discussions.

Our paper builds on earlier work by Salem et al. and Stuyver et al. in terms of formally characterising the states as diradical and zwitterionic within a two-orbital two-electron model (TOTEM). On top of this, we have provided practical protocols for recognising these states in realistic computations. Using our tools in the case of the para-quinodimethane molecule as a model system, we show that it is possible to identify the states arising from the TOTEM but also that the π-conjugated bridge plays a crucial role producing more complicated states than one would have expected from the simple TOTEM.

Matrix-free hyperfluorescence

Felix

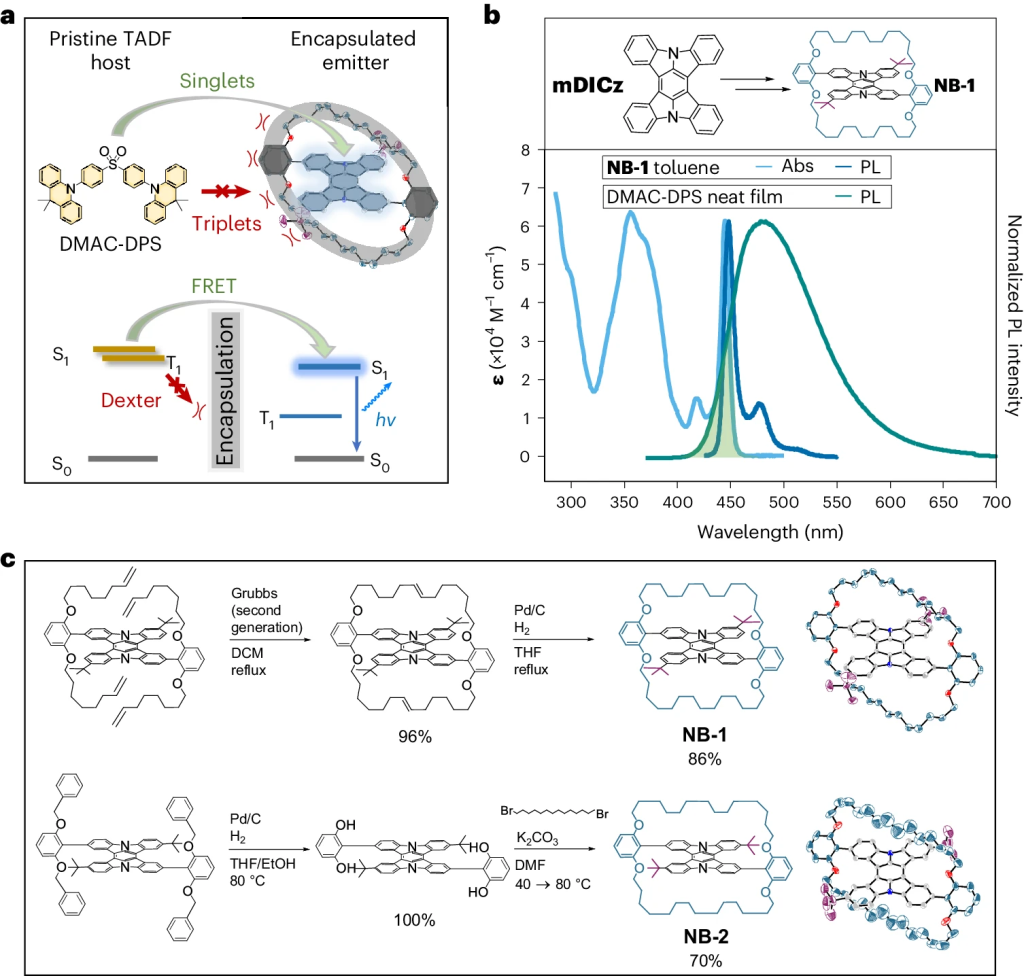
Hyperfluorescence is an emerging technique for generating highly efficient OLEDs by combining a triplet harvester with a bright emitter molecule. Current devices are overly complex due to the number of components involved hampering practical application. A new paper, led by Hugo Bronstein from the University of Cambridge presents an important step toward solving this problem. The idea is to encapsulate the emitter, thus, avoiding the need for a high-gap matrix. The approach is presented in the paper Suppression of Dexter transfer by covalent encapsulation for efficient matrix-free narrowband deep blue hyperfluorescent OLEDs, which just appeared in Nature Materials.

Post-Doc Position on the Dynamics of High-Energy Materials

Felix

Applications are invited for a postdoctoral research associate position in computational chemistry at Loughborough University. This is a DSTL funded position to work with Dr Kenny Jolley and Dr Felix Plasser (Chemistry, Loughborough University) on predicting the crystal structure, dynamics and physical properties of energetic materials.

The successful applicant will conduct molecular dynamics (MD) and accelerated MD simulations on energetic compounds. Bulk physical properties, stability to shock and heat, and reaction pathways will be modelled and compared to experimental data. In a later stage, we will perform time-resolved simulations of explosion processes.

This position is ideally suited for an ambitious early career researcher with a background in computational chemistry and materials modelling. The successful candidate will be highly motivated with a strong research track record and a desire to pursue multidisciplinary research.

Feel free to contact me or Dr Kenny Jolley for informal equiries.

Closing date for applications is 24/11/2023, please follow this link for further info.

Ionic states

Felix

Our new paper Quantification of the Ionic Character of Multiconfigurational Wave Functions: The Qat Diagnostic just appeared in the Journal of Physical Chemistry A.

The paper deals with the fact that the widely used CASSCF method, if not used carefully, can yield large errors (1-2 eV) in vertical excitation energies. This problem arises for ionic states, as defined within valence bond theory. Within this work we developed a simple diagnostic to identify ionic states. We found a good correlation between the new diagnostic (Qta) and the error, as shown in the figure above.

We hope that the new diagnostic will be useful similar to analogous diagnostics identifying charge transfer states in TDDFT computations. This will give users the possibility to spot potential problems quickly.

On-going work is concerned with going from just diagnosing the problem to developing a numerical correction term to fix the problem.